Spin Angular Momentum Operator In Quantum Mechanics
I am trying to compile a list of fundamental commutation relations involving position, linear momentum, total angular momentum, orbital angular momentum, and spin angular momentum.
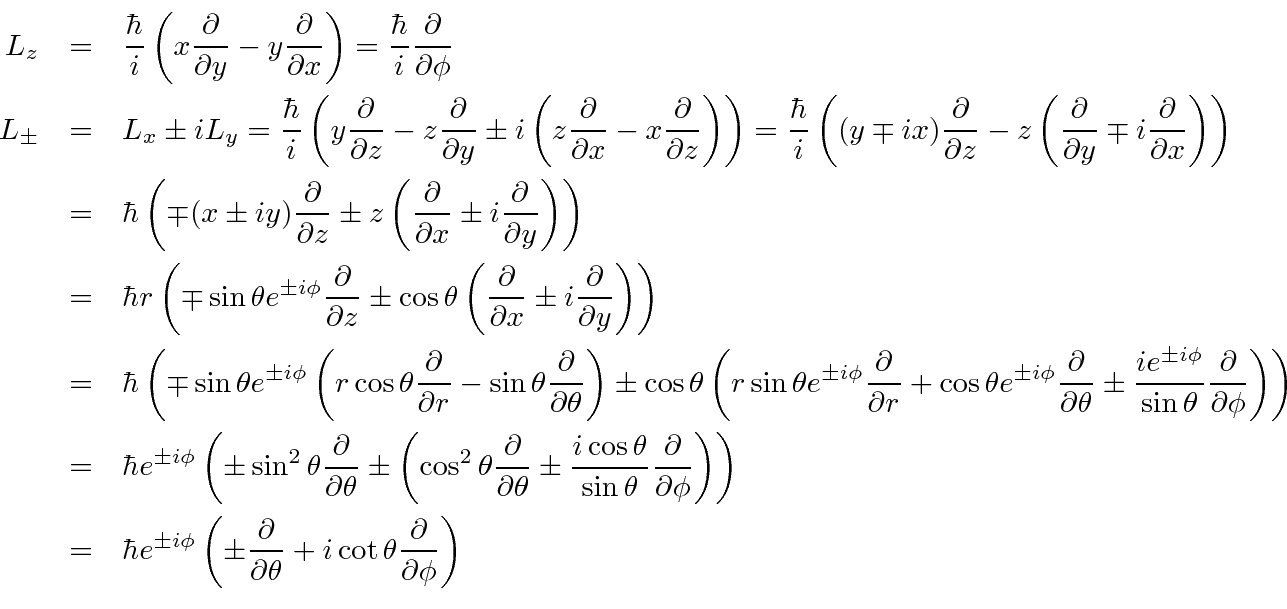
Spin angular momentum operator in quantum mechanics. Operators Matrices and Spin We have already solved many problems in Quantum Mechanics using wavefunctions and differential operators. Course Prerequisite(s) EN.615.641. The sum of operators is another operator, so.
Since the eigenfunctions of Hermitian operators are orthogonal (and we normalize them) we can now use the standard linear algebra to solve quantum problems with vectors and matrices. In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors.A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics.The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical. A particle without angular momentum looks the s.
I Li = xˆiǫijk xˆj pˆk = ǫijk xˆi xˆj pˆk = 0. According to Section 2.5, in quantum mechanics, we can always adopt the Schrödinger representation, for which ket space is spanned by the simultaneous eigenkets of the position operators, , , and , and takes the form. Angular Momentum in Quantum Mechanics Asaf Pe’er1 April 19, 18 This part of the course is based on Refs.
Now in Quantum Mechanics (QM) it should not shock you to learn particles also have orbital and spin angular momentum (the sum of these two is the again total angular momentum for the particle). Previous index next PDF. Spin Angular Momentum Previous:.
The matrix forms of the spin angular momentum operator (s = 1) in the (s2, s,) representation, in which s2, s, are diagonal, are Direct calculation gives 1 0 s;= 0 0 0 0 0 4 0 sv=$ ;. In quantum mechanics, angular momentum is defined analogously to classical angular momentum and, like it, can be divided into orbital angular momentum and spin. Formulation of quantum mechanics shows that particles can exhibit an intrin-sic angular momentum component known as spin.
Be aware that I will not distinguish a classical quantity such as x from the corresponding. A quantum state is an abstract description of a particle. To demonstrate that this association of m with the z-component of angular momentum is indeed correct, we need to write an operator for the z-component of angular momentum.
Identical to angular momentum states, i.e., we will nd that the algebraic properties of operators governing spatial and spin rotation are identical and that the results derived for products of angular momentum states can be applied to products of spin states or a combination of angular momentum and spin states. These are the components. In QM, orbital angular momentum is associated with a particle that is interacting with another particle (these interacting particles form what’s.
A spin of 1 / 2 means that the particle must be fully rotated twice (through 7°) before it has the same configuration as when it started. 7 Hydrogen atom and hidden symmetry 9. Eigenstates of and Up:.
Spin is an intrinsic property of a particle. There are also some operators that do not have a classical counterpart (remember that quantum-mechanics is more. L z = XP y ¡YP x:.
We will find later that the half-integer angular momentum states are used for internal angular momentum (spin), for which no or coordinates exist. Spin angular momentum operators cannot be expressed in terms of position and momentum operators, like in Equations -, because this identification depends on an analogy with classical mechanics, and the concept of spin is purely quantum mechanical:. Of the orbital angular momentum L and the spin angular momentum S:.
An important case of the use of the matrix form of operators is that of Angular Momentum Assume we have an atomic state with (fixed) but free. We will now show that precisely the same result appears in the study of the quantum mechanics of an electron spin in a magnetic field. We may use the eigenstates of as a basis for our states and operators.
Likewise, the spin angular momentum operators cannot be represented as differential. This course presents the basic concepts and mathematical formalism of quantum mechanics. In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum.The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry.In both classical and quantum mechanical systems, angular momentum (together with linear momentum and energy) is.
To formulate our quantum operators. And the angular momentum operators L. Take for example the dot product of r with L to get.
3002 The three matrix operators for spin one satisfy sz sy - sy s, = i sz and cyclic permutations. The rotation operator (,), with the first argument indicating the rotation axis and the second the rotation angle, can operate through the translation operator for infinitesimal rotations as explained below. Therefore, the eigenstate is.
Thus, by analogy with Section s8.2 , we would expect to be able to define three operators—\(S_x\), \(S_y\), and \(S_z\)—that represent the three Cartesian components of spin angular momentum. Many problems in Quantum Mechanics are solved by limiting the calculation to a finite, manageable, number of states, then finding the linear combinations which are the. Hence, we will need to build up our quantum mechanics toolbox just a little more (more information about spin in the course 'quantum mechanics II').
1 Adding apples to oranges?. The spin operator, S, represents another type of angular momentum, associated with “intrinsic rotation” of a particle around an axis;. Ignoring the (fixed) radial part of the wavefunction, our state vectors for must be a linear combination of the.
Unlike regular wavefunctions, spin wavefunctions do not exist in real space. In classical physics, angular momentum describes a movement. The classical momentum conjugate to the azimuthal angle is the -component of angular momentum,.
The angular momentum vector L, with magnitude \( \sqrt{\ell ({\ell +1}) } \hbar \), can be pictured as precessing about the z-axis, with its z-component \( L_z \) constant. Operators Matrices and Spin Previous:. ˆ y, L ˆ z.
Since angular momentum results from rotation about an axis, it seems plausible that the mJ quantum number is related to the z-component of angular momentum. In quantum mechanics and particle physics, spin is an intrinsic form of angular momentum carried by elementary particles, composite particles (), and atomic nuclei. The energy operator is called Hamiltonian (this is also true in classical mechanics) and is usually denoted by the symbol H.
However, the discovery of the spin degree of freedom marginally predates the development of rela-tivistic quantum mechanics by Dirac and was acheived in a ground-breaking experiement by Stern and Gerlach (1922). Show that 3_s, - sz, (sz &is,)3 = 0. However, it has long been known that in quantum mechanics, orbital angular momentum is not the whole story.Particles like the electron are found experimentally to have an internal angular momentum, called spin.
Topics include the mathematics of quantum mechanics, the harmonic oscillator and operator methods, quantum mechanics in three dimensions and angular momentum, quantum mechanical spin, quantum statistical mechanics, approximation methods, and quantum theory of scattering. We may add the spin angular momentum S of a particle to its orbital angular momentum L. The mathematical structure of angular momentum in quantum mechanics led to spherical.
Even though the probability may be single valued, discontinuities in the amplitude would lead to infinities in the Schrödinger equation. The manuscript also ponders on functions used in quantum mechanics, relativistic quantum mechanics, and radiation theory. L y = ZP x ¡XP z;.
The classical angular momentum operator is orthogonal to both lr and p as it is built from the cross product of these two vectors. While we can make product states where we know each particles spin-there by justifying an $8 \times 8$ operator, those states are not eigenstates of total angular momentum, and hence we don't want to consider them. Angular momentum is the vector sum of the components.
The spin number describes how many symmetrical facets a particle has in one full rotation;. R · L = xˆ ˆ. Angular momentum is a necessary consequence of physics in 3 dimensions.
In quantum mechanics, however, it describes a symmetry, namely the rotational symmetry of an object, or more precisely:. The quantum-mechanical behavior of the angular momentum and its components can be represented by a vector model, illustrated in Figure 5. This book offers a concise introduction to the angular momentum, one of the most fundamental quantities in all of quantum mechanics.
Because spin is a type of angular momentum, it is reasonable to suppose that it possesses similar properties to orbital angular momentum. The corresponding operator is bS. In quantum mechanics, angular momentum is a vector operator of which the three components have well-defined commutation relations.This operator is the quantum analogue of the classical angular momentum vector.
Thus, by analogy, we would expect to be able to define three operators that represent the three Cartesian components of spin angular momentum. Operator, and the difierence of operators is another operator, we expect the components of angular momentum to be operators. The coherent states of a simple harmonic oscillator discussed.
We have already seen an example of this:. Beginning with the quantization of angular momentum, spin angular momentum, and the orbital angular momentum, the author goes on to discuss the Clebsch-Gordan coefficients for a two-component system. The $8 \times 8$ matrix indicates a misunderstanding of the problem:.
2 General properties of angular momentum operators 2.1 Commutation relations between angular momentum. Intrinsic and total angular momentum Orbital angular momentum is not the only source of angular momentum, particles may have intrinsic angular momentum or spin. In other words, quantum mechanically L x = YP z ¡ZP y;.
The eigenvalues of bS2 have the same form as in the orbital case, ~2s(s+ 1), but now scan be integer or half integer;. As a warm up to analyzing how a wave function transforms under rotation, we review the effect of linear translation on a single particle wave function ψ (x). This is why, it is first shown how the translation operator is acting on a particle at position x (the particle is then in the state | according to Quantum Mechanics).
( Wisconsin) 174 Problems and Solutions on Quantum Mechanics Solution:. In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum.The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry.In both classical and quantum mechanical systems, angular momentum (together with linear momentum and energy) is. In this lecture, we will start from standard postulates for the angular momenta to derive the key characteristics highlighted by the Stern-Gerlach experiment.
The components \( L_x \) and \( L_y. The Angular Momentum Matrices* Contents It is often convenient to solve eigenvalue problems like using matrices. We are going to be adding angular momenta in a variety of ways.
Matrix Representation of Angular Momentum David Chen October 7, 12 1 Angular Momentum In Quantum Mechanics, the angular momentum operator L = r p = L xx^+L yy^+L z^z satis es L2 jjmi= ~ j(j+ 1)jjmi (1) L z jjmi= ~ mjjmi (2) The demonstration can be found in any Quantum Mechanics book, and it follows from the commutation relation r;p = i~1. J = L + S. The extrinsic angular momentum, on the other hand, can be visibly and even classically observed.
Similarly the eigenvalues of Sb z. Or we may want to add the spin. 1 Angular momentum in Quantum Mechanics As is the case with most operators in quantum mechanics, we start from the clas-sical definition and make the transition to quantum mechanical operators via the standard substitution x → x and p → −i~∇.
Atomic energy levels are classifled according to angular momentum and selection rules for ra-diative transitions between levels are governed by angular-momentum addition rules. Angular momentum entered quantum mechanics in one of the very first—and most important—papers on the "new" quantum mechanics, the Dreimännerarbeit (three men's work) of Born. In this article, we will be dealing with spin-1/2.
An System in a Up:. 6 General aspects of addition of angular momentum 9. Happily, these properties also hold for the quantum angular momentum.
Topics include variational method, stationary state perturbation theory, isotopic spin, second quantization, properties of angular momentum operators, and angular momentum and rotations of coordinate axes. In quantum mechanics, spin is an intrinsic property of all elementary particles.All known fermions, the particles that constitute ordinary matter, have a spin of 1 / 2. Quantum Generalization of the Rotation Operator.
The Angular Momentum Matrices *. In the vivid classical model, orbital angular momentum describes the movement of a par. Angular momentum vector L precesses about magnetic field direction with angular velocity ω 0 = −γB (independent of angle).
Analyzing this intrinsic 'spin' component is not very intuitive;. I.e., it has no analogy in classical physics. Angular Momentum Understanding the quantum mechanics of angular momentum is fundamental in theoretical studies of atomic structure and atomic transitions.
Angular Momentum Operator Algebra. Spin is one of two types of angular momentum in quantum mechanics, the other being orbital angular momentum.The orbital angular momentum operator is the quantum-mechanical counterpart to the classical angular momentum of orbital. The state describes probability distributions for the observables of the particle, such as angular momentum, linear momentum, etc.
Spin Operators Spin Space We now have to discuss the wavefunctions upon which the previously introduced spin operators act.

Angular Momentum In Quantum Mechanics Investigations In Physics 10 Edmonds A R Amazon Com Books
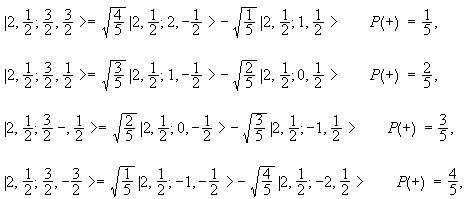
Addition

Why Do We Relate Spin With Angular Momentum Operator In Quantum Me
Spin Angular Momentum Operator In Quantum Mechanics のギャラリー

Angular Momentum Ladder Operators
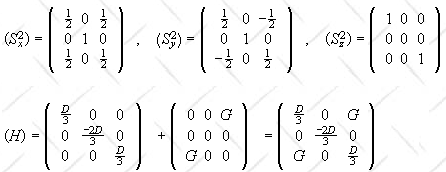
Problems
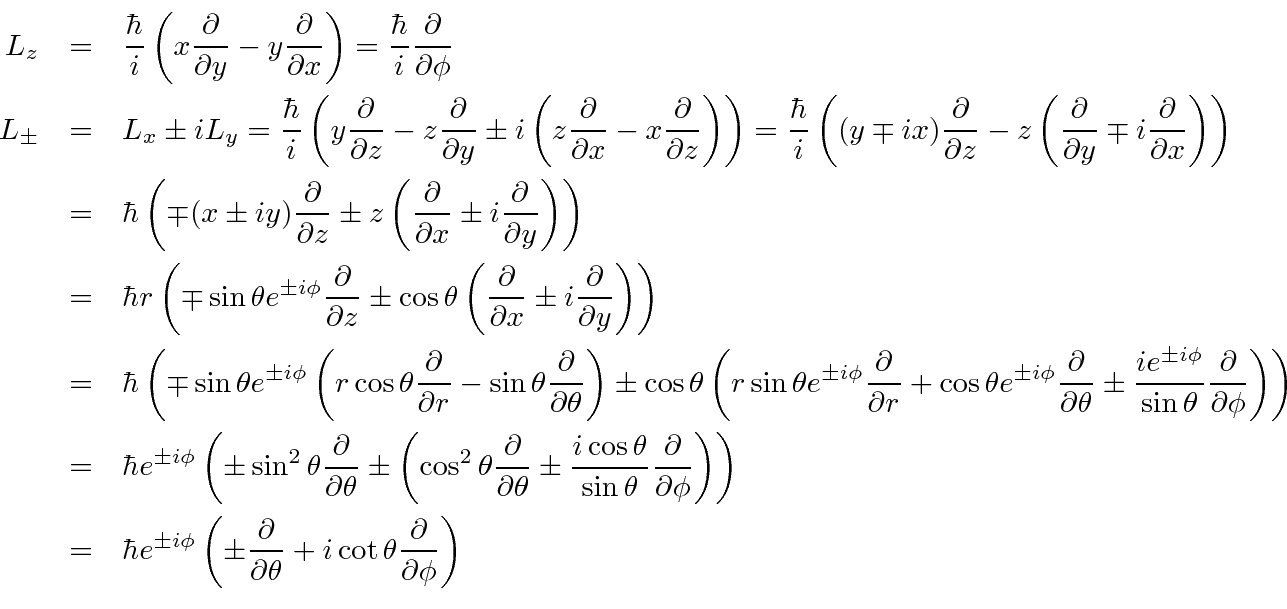
Spherical Coordinates And The Angular Momentum Operators

Quantum Mechanics Volume 2 Angular Momentum Spin And Approximation Methods 2nd Edition Wiley
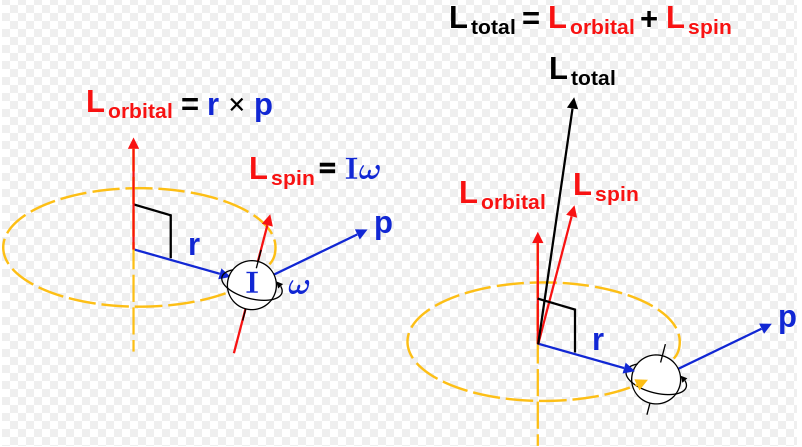
Quantum Diaries
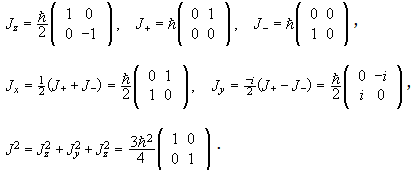
Properties
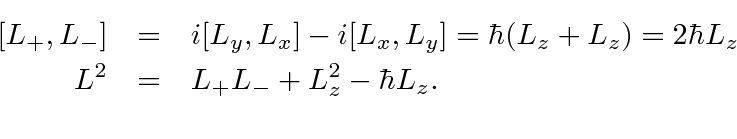
Angular Momentum Algebra Raising And Lowering Operators
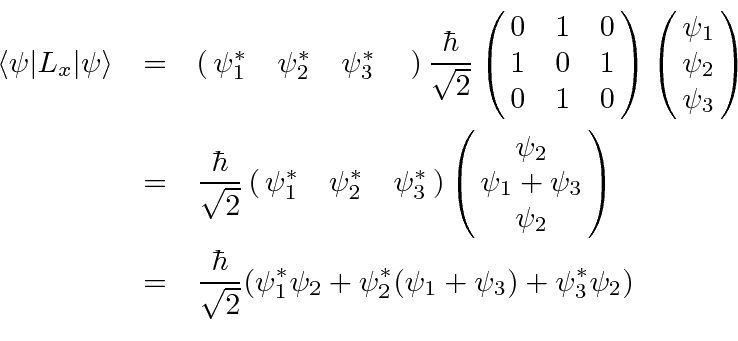
The Angular Momentum Matrices

Physics Ch 66 5 Quantum Mechanics The Hydrogen Atom 36 Of 78 Spin Angular Momentum Youtube

Solved 2 10 Points In Quantum Mechanics The Operators Chegg Com
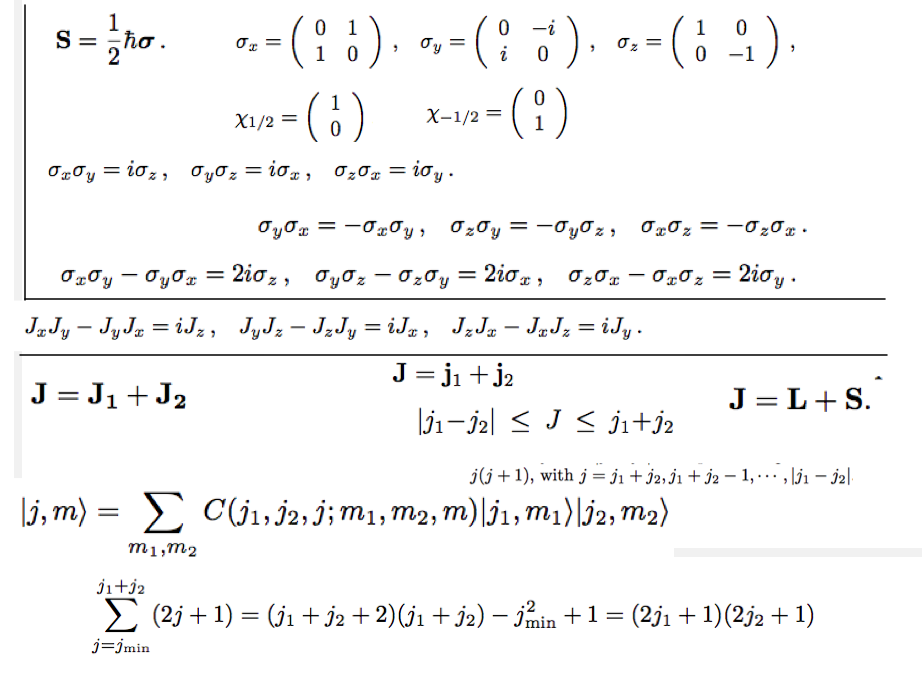
Atomic Physics Part Phys261
Http Www Tcm Phy Cam Ac Uk s10 Aqp Lec4 Compressed Pdf

Spin In Quantum Mechanics Youtube

Spin 3 2 The Spectrum Of Riemannium
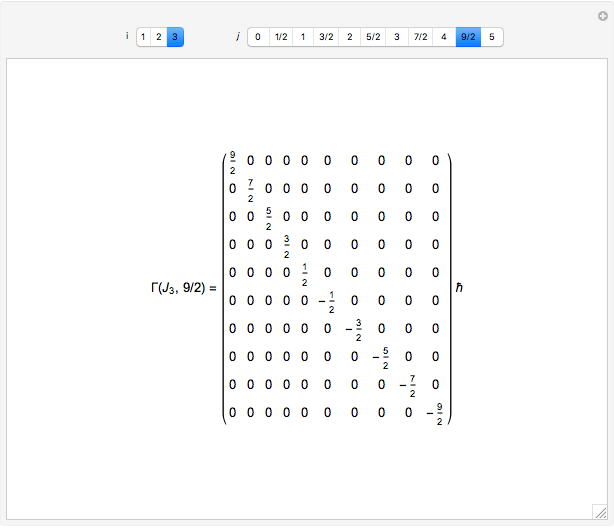
Quantum Angular Momentum Matrices Wolfram Demonstrations Project

Quantum Mechanics Of Angular Momentum Ppt Download
Angular Momentum Operator Quantum Mechanics Spin Png 1280x948px Angular Momentum Operator Angular Momentum Area Art Bohr

Orbital Angular Momentum Ppt Video Online Download
Q Tbn 3aand9gcthfjdsquv1pylym8k68d5c Vk92cxxpokoxdodxybfo2im4cqe Usqp Cau

Quantum Angular Momentum Operators Physical Chemistry Angular Momentum

Pdf Angular Momentum And Spin In Quantum Mechanics A Review Dr J M Ashfaque Amima Minstp Academia Edu

Angular Momentum Operator 978 613 2 5
Q Tbn 3aand9gcs3xwob4rjd6x Aqfrtpzfzxvorv2 Sat560 Labii9lbpv243j Usqp Cau

Spin And Addition Of Angular Momentum Ppt Video Online Download

Total Angular Momentum An Overview Sciencedirect Topics

Solved I Am Confused With Q4 You Don T Have To Do Q3 Q3 Chegg Com
Http Link Springer Com Content Pdf 10 1007 2f0 306 X 1 Pdf

Spin 1 2 Youtube

Lecture 5 Orbital Angular Momentum Spin And Rotation 1

Angular Momentum Operator Wikipedia
What Is Angular Momentum In Quantum Mechanics Quora

Angular Momentum Operator Wikipedia
Onlinelibrary Wiley Com Doi Pdf 10 1002 App2

Solved 8 In Quantum Mechanics The Spin Of The Electron Chegg Com

Angular Momentum
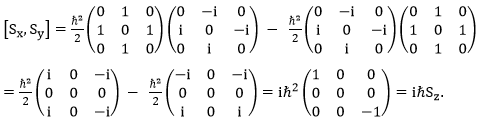
Properties

Quantum Theory Of Angular Momentum Angular Momentum Operators Pdf Document

Chapter 11 Angular Momentum General Theory
Q Tbn 3aand9gcqx Gjvxrrqdiu49v40wbszetypi14zlrt9lx2qn1h Kiqxbm Usqp Cau

Ppt 16 Angular Momentum Powerpoint Presentation Free Download Id
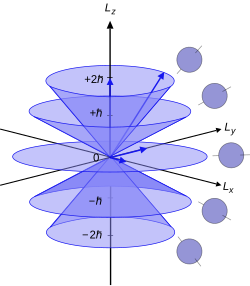
Angular Momentum Operator Wikipedia

Solved Quantum Mechanics Spin 3 2 Angular Momentum Show Chegg Com

Angular Momentum Operator Introduction To Quantum Mechanics Exam Docsity

Ppt Spin And Addition Of Angular Momentum Powerpoint Presentation Free Download Id

Solved 8 In Quantum Mechanics The Spin Of The Electron Chegg Com

Ppt Orbital Angular Momentum Powerpoint Presentation Free Download Id 5878

Angular Momentum Book Chapter Iopscience

Quantum Mechanics 4 Angular Momentum And Spin Lecture Notes And Qs Studocu

Quantum Mathematics 34 4 Operators For Spin Angular Momentum Youtube

Physics 543 Quantum Mechanics Ii University Of Calgary
Q Tbn 3aand9gcstj0qwwtacmumilp2lqfi9izwvogbljxvwbsdzfxijtsll8k9r Usqp Cau

Pdf Angular Momentum In Quantum Mechanics Omer Gassim Academia Edu

Angular Momentum Book Chapter Iopscience

Atomic Physics Part Phys261

Vector Model Of Angular Momentum
Http Joelcorbo Com Docs Notes Spin Pdf
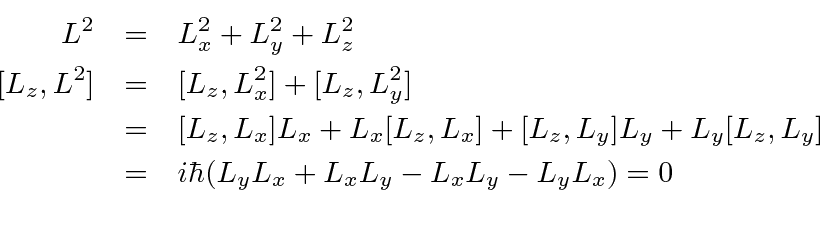
The Commutators Of The Angular Momentum Operators

Adding 3 Electron Spins Physics Stack Exchange

Angular Momentum Eigenfunctions Youtube

Pdf On Angular Momentum Operator In Quantum Field Theory

The Dirac Equation Spin And Open Access To The Royal Society Transactions And Proceedings
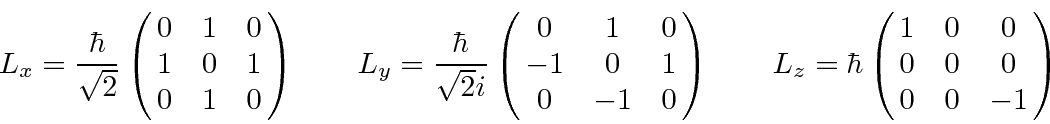
The Angular Momentum Matrices
Ocw U Tokyo Ac Jp Lecture Files Engin 06 1 Notes En 2 1e Pdf

Angular Momentum Notes

Quantum Angular Momentum Book Chapter Iopscience
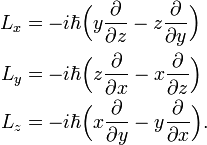
Angular Momentum Quantum Knowino

Spin Physics Wikipedia

Introduction To Quantum Mechanics Pages 151 0 Flip Pdf Download Fliphtml5

P460 Spin1 Spin And Magnetic Moments Skip Sect 10 3 Orbital And Intrinsic Spin Angular Momentum Produce Magnetic Moments Coupling Between Moments Ppt Download
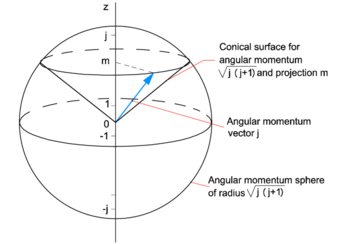
Angular Momentum Quantum Knowino

Angular Momentum Operator Wikiwand

Angular Momentum Operator Algebra Youtube
Www Studocu Com En Gb Document University Of Hertfordshire Physics Lecture Notes Quantum Mechanics 4 Angular Momentum And Spin Lecture Notes And Qs View

Quantum Mechanics 7b Angular Momentum Ii Youtube
Arxiv Org Pdf 03
Www3 Nd Edu Johnson Class01f Chap1a Pdf

Part Iii Quantum Mechanics
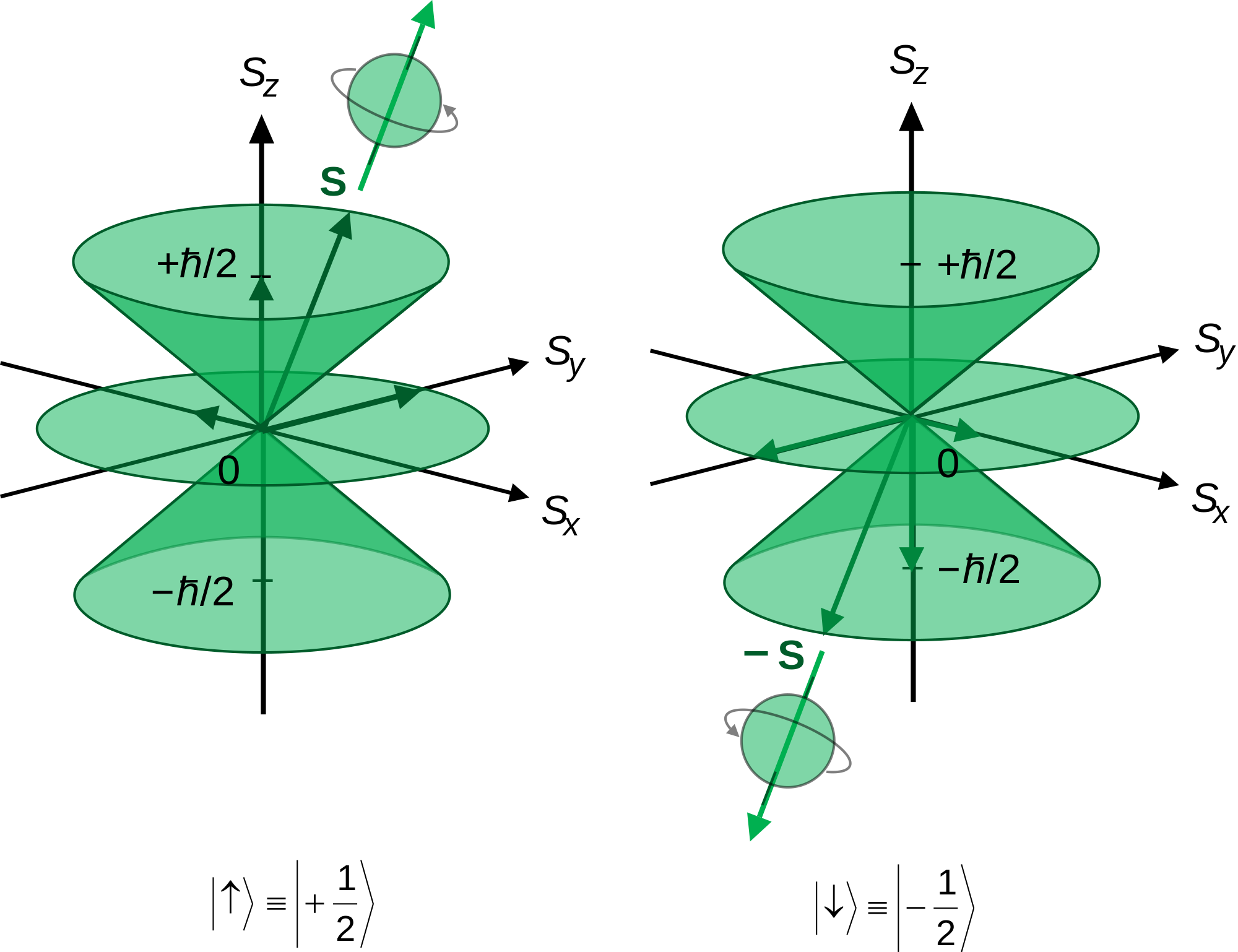
Where Exactly Do The Orbital Angular Momentum Get Their Numbers E G 1 2 Chemistry Stack Exchange

Amazon Com Mcqs 4 Angular Momentum And Spin Mcqs In Quantum Mechanics Ebook Singh Sardar Kindle Store

Eigenfunctions Of Angular Momentum Part 1 Youtube

Quantum Angular Momentum

Solved 2 1 The Spin Operators This Is A Problem On Vecto Chegg Com
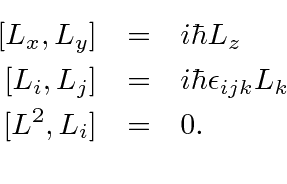
Angular Momentum Algebra Raising And Lowering Operators

Angular Momentum Book Chapter Iopscience

Angular Momentum Notes

Pdf Angular Momentum And Spin Dr J M Ashfaque Amima Minstp Academia Edu

Atomic Physics Part Phys261

Spin Orbit Coupling
Faculty Biu Ac Il Barkaie Hw10 Pdf

Ppt Angular Momentum In Quantum Mechanics Powerpoint Presentation Free Download Id

Angular Momentum Operators

Orbital Angular Momentum Ppt Download

Ppt Angular Momentum In Quantum Mechanics Powerpoint Presentation Free Download Id

Parallel Construction Between The Qunatum Mechanics Of Angular Momentum Download Scientific Diagram

Pdf Angular Momentum In Quantum Mechanics

Pdf Quantum Mechanics 2 Lecture Notes
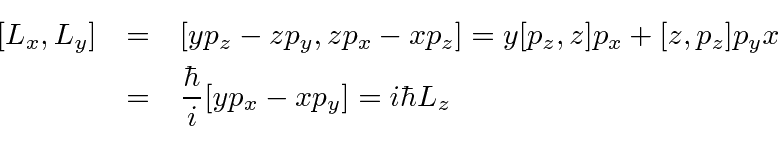
The Commutators Of The Angular Momentum Operators

Quantum Angular Momentum

Angular Momentum

Solved 8 In Quantum Mechanics The Spin Of The Electron Chegg Com

Part Iii Quantum Mechanics



