Spin Angular Momentum Operator
In the "uncoupled basis” the states are of the form |m1m2mzma) where m 1,2,3,4 = +1 denotes the eigenvalue of ħ-1Sız, etc.

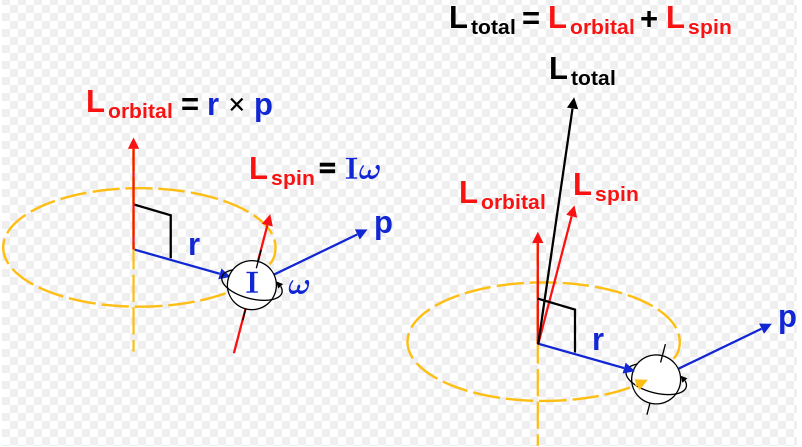
Spin angular momentum operator. The orbital angular momentum operator is the quantum-mechanical counterpart to the classical angular momentum of orbital revolution and appears when there is periodic structure to its wavefunction as the angle varies. Orbital angular momentum (a 5s state). These matrices are called the Pauli matrices.
Is the spin-1 operator of the photon with the SO(3) rotation generators. The classical angular momentum operator is orthogonal to both lr and p as it is built from the cross product of these two vectors. Thus, by analogy with Sect.
Now consider following operator:. We can show that mathL_x/math is Hermitian by directly evaluating its adjoint and showing that it’s equal to mathL_x/math, using the fact that the adjoint operator is antilinear and antidistributive:. (1) The matrices must satisfy the same commutation relations as the differential operators.
K = cos Ꮎ Ꭻ + sin Ꮎ Ꭻy. In 1940, Wolfgang Pauli proved the so-called spin-statistics theorem using relativistic quantum. Or we may want to add the spin.
The operators (ˆSx, ˆSy, ˆSz) are Hermitian because they represent the physical quantity of spin, orbital, or resultant angular momentum, and the operators (ˆSx, ˆSy, ˆSz) are Hermitian mathematically because they are equal to their respective complex conjugate transposes. Thus a magnetic dipole moment is also that of the last electron (the nucleus has much smaller dipole moment and can be ignored). The classical expression for the z-component of angular momentum is \ M_z = xp_y - yp_x \label {7-38}\ By substituting the equivalents for the coordinates and momenta we obtain.
Moreover, it is plausible that these operators possess analogous commutation relations to the three corresponding orbital angular momentum operators, , , and see Eqs. The spin operators are an (axial) vector of matrices. An intrinsic angular momentum component known as spin.
To begin with, let us define the ladder (or raising and lowering) operators J + = J x +iJ y. Spin is often depicted as a particle literally spinning around an axis, but this is only a metaphor:. Angular momentum raising and lowering operators from rect-angular coordinates Pingback:.
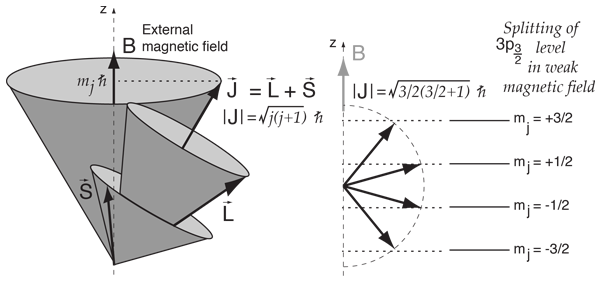
We can easily derive the matrices representing the angular momentum operators for. The spin rotation operator:. The total angular momentum J is the sum of the orbital angular momentum L and the spin angular momentum S:.
(6) (a) Explain how to write down Ją and Jy in the eigenbasis of J2 (the standard basis), by using the raising and lowering operators for angular momentum (J+). The important feature of the spinning electron is the spin angular momentum vector, which we label \(S\) by analogy with the orbital angular momentum \(L\). 7 Hydrogen atom and hidden symmetry 9.
I.e., it has no analogy in classical physics. We define the total spin operators. This is why, it is first shown how the translation operator is acting on a particle at position x (the particle is then in the state | according to Quantum Mechanics).
Clebsch-Gordan coefficients for addition of spin-1/2 and gen-eral L. (6.19) h S~2;S i i = 0 :. Spin angular momentum operators cannot be expressed in terms of position and momentum operators, like in Equations -, because this identification depends on an analogy with classical mechanics, and the concept of spin is purely quantum mechanical:.
We have not encountered an operator like this one, however, this operator is comparable to a vector sum of operators;. However, it has long been known that in quantum mechanics, orbital angular momentum is not the whole story.Particles like the electron are found experimentally to have an internal angular momentum, called spin. The Commutators of the Angular Momentum Operators however, the square of the angular momentum vector commutes with all the components.
It is convenient to adopt the viewpoint, therefore, that any vector operator obeying these characteristic commuta-tion relations represents an angular momentum of some sort. We’ve already established that the rotation operator, acting on the two spin system, can be represented by a \(4\times 4\) matrix, and that the new (total angular momentum) basis can be reached from the original (two separate spin) basis by the orthogonal transformation given explicitly above. There is another type of angular momentum, called spin angular momentum (more often shortened to spin), represented by the spin operator S.
However, the discovery of quantum mechanical spin predates its theoretical understanding, and appeared as a result of an ingeneous experiment due to Stern and Gerlach. We are going to be adding angular momenta in a variety of ways. Consider 4 distinguishable spin-degrees of freedom, with the spin angular momentum operators S1,2,3,4 acting on each distinct spin.
(7.17) The spin observable squared also commutes with all the spin components, as in Eq. J = L + S. Spin is one of two types of angular momentum in quantum mechanics, the other being orbital angular momentum.
The total angular momentum operator for the two electrons is given by where is the total spin angular momentum operator for the first two particles, S, is the spin operator for the jth particle and L2 is the orbital angular momentum operator for the second electron (we neglect the orbital angular moment of electron 1 since it is in the に0. It is essentially a ket with operator components. In both classical and quantum mechanical systems, angular momentum (together with linear momentumand energy) is one of the three fundamental properties of motion.
As it turns out, the angular momentum is completely described in terms of the position and momentum (in the x, y, z directions) of the particle. \begin{equation} exp\left(\frac{-i\sigma\cdot\textbf{n}\phi}{2}\right) \end{equation} For a $\pi$ rotation around $\textbf{x}$ the rotation matrix takes form \begin{pmatrix} 0 & -i \\ -i & 0. In other words, spin has no analogy in classical physics.
Spherical harmonics using the lowering operator Pingback:. I Li = xˆiǫijk xˆj pˆk = ǫijk xˆi xˆj pˆk = 0. ORBITAL ANGULAR MOMENTUM - SPHERICAL HARMONICS 3 Since J+ raises the eigenvalue m by one unit, and J¡ lowers it by one unit, these operators are referred to as raising and lowering operators, respectively.
Moreover, it is. All we know is that it obeys the commutation relations J i,J j = i~ε ijkJ k (1.2a) and, as a consequence, J2,J i = 0. R · L = xˆ ˆ.
All the orbital angular momentum operators, such as L x, L y, and L z, have analogous spin operators:. And the commutation relations work the same way for spin:. Spin angular momentum operators cannot be expressed in terms of position and momentum operators, like in Equations -, because this identification depends on an analogy with classical mechanics, and the concept of spin is purely quantum mechanical.
Quantum Generalization of the Rotation Operator. There is no equivalent representation of the corresponding spin angular momentum operators. We may add the spin angular momentum S of a particle to its orbital angular momentum L.
Spectrum and structure of the eigenstates of angular momentum. The spin operator, S, represents another type of angular momentum, associated with “intrinsic rotation” of a particle around an axis;. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry.
The last two lines state that the Pauli matrices anti-commute. The rotation operator (,), with the first argument indicating the rotation axis and the second the rotation angle, can operate through the translation operator for infinitesimal rotations as explained below. In any case, among the angular momentum operators L x, L y, and L z, are these commutation relations:.
(a) Show that į į į Ⓡ }= 2. Lets just compute the commutator. In this lecture, we will start from standard postulates for the angular momenta to derive the key characteristics highlighted by the Stern-Gerlach experiment.
6 General aspects of addition of angular momentum 9. Spin operators and Pauli matrices. Where γ i is the magnetogyric ratio of the ith nucleus, and I Zi is the component along Z of the nuclear spin angular momentum operator, I i.
Hence, we conclude that there is no reason why the quantum number \(s\) cannot take half-integer, as well as integer, values. 1 Adding apples to oranges?. The sum of operators is another operator, so angular momentum is an operator.
First of all the parity operator commutes with the spin, so that doesn't affect it, and you just have to think about the rotation around x. For spin, J = S =1 2!σ, and the rotation operator takes the form1eiθˆn·J/!=ei(θ/2)(nˆ·σ). Spin is an intrinsic property of a particle, unrelated to any sort of motion in space.
This will give us the operators we need to label states in 3D central potentials. Broadly speaking, a classical extended object ( e.g., the Earth) can possess two different types of angular momentum. Take for example the dot product of r with L to get.
Because spin is a type of angular momentum, it is reasonable to suppose that it possesses similar properties to orbital angular momentum. Angular momentum is the vector sum of the components. These obey the same commutation relations as other angular momentum operators.
We thus generally say that an arbitrary vector operator J~ is an angular momentum if its Cartesian components are. We might write fl flL > = 0 @ L. To take account of this new kind of angular momentum, we generalize the orbital angular momentum ˆ→L to an operator ˆ→J which is defined as the generator of rotations on any wave function, including possible spin components, so R(δ→θ)ψ(→r) = e − i ℏδ→θ.
We will also review below the well-known fact that spin states under rotations behave essentially identical to angular momentum states, i.e., we will nd that the algebraic properties of operators governing spatial and spin rotation are identical and that the results derived for products of angular momentum states can be applied to products of spin states or a combination of angular momentum and spin states. The only possible angular momentum is the intrinsic angular momentum of the last electron. Happily, these properties also hold for the quantum angular momentum.
We know the quantum operators of position and momentum and can just substitute them in to find the angular momentum quantum operator. The silver is vaporized in an oven and. Total J for sum of two angular momenta Pingback:.
Math\begin{align*} L_x^\dagger &= (yp. 8.2, we would expect to be able to define three operators--, , and --which represent the three Cartesian components of spin angular momentum. 2 General properties of angular momentum operators 2.1 Commutation.
Since spin is some kind of angular momentum we just use again the Lie algebra 3, which we found for the angular momentum observables, and replace the operator ~Lby S~ S i;S j = i~ ijkS k:. We define spin angular momentum operators with the same properties that we found for the rotational and orbital angular momentum operators. We create an angular momentum operator by changing the classical expression for angular momentum into the corresponding quantum mechanical operator.
It is common to define the Pauli Matrices, , which have the following properties. Take the rotation operator written in the Pauli formalism:. Furthermore, since J 2 x + J y is a positive deflnite hermitian operator, it follows that.
Representing the Rotation Operator in the Total Angular Momentum Basis. The corresponding spin operators are These satisfy the usual commutation relations from which we derived the properties of angular momentum operators. It is easy to derive the matrix operators for spin.
Matrix Representation of Angular Momentum David Chen October 7, 12 1 Angular Momentum In Quantum Mechanics, the angular momentum operator L = r p = L xx^+L yy^+L z^z satis es L2 jjmi= ~ j(j+ 1)jjmi (1) L z jjmi= ~ mjjmi (2) The demonstration can be found in any Quantum Mechanics book, and it follows from the commutation relation r;p = i~1. The first type is due to the rotation of the object’s center of mass about some fixed external point ( e.g., the Sun)—this is generally known as orbital angular momentum. Angular momentum operator by J.
The second type is due to the object’s internal motion—this is generally known as spin angular momentum (because, for a rigid object, the internal motion consists of spinning about an axis passing. Since spin is a type of angular momentum, it is reasonable to suppose that it possesses similar properties to orbital angular momentum. The important feature is that this Hamiltonian has an identical form in both isotropic and anisotropic systems, and hence the spectral consequences are exactly the same.
Total-s matrix and eigenstates in product basis Pingback:. The sum of angular momentum will be quantized in the same way as orbital angular momentum. Because of this, the quantum-mechanical spin operators can be represented as simple 2 × 2 matrices.
The spin angular momentum of light (SAM) is the component of angular momentum of light that is associated with the quantum spin and the rotation between the polarization degrees of freedom of the photon. Creation and annihilation operators can be constructed for spin-1 / 2 objects;. S x, S y, and S z.
This is a very important result since we derived everything about angular momentum from the commutators. (1.2b) Remarkably, this is all we need to compute the most useful properties of angular momentum. These satisfy the usual commutation relations from which we derived the properties of angular momentum operators.
View chapter Purchase book. In general, the rotation operator for rotation through an angleθabout an axis in the direction of the unit vector ˆn is given byeiθnˆ·J/!where J denotes the angular momentum operator. ( 531 )- ( 533 ).
Its easy to show the total spin operators obey the same commutation relations as individual spin operators audio. Consider a particle of spin j = 1, with angular momentum matrices Jr, Jy and Jz. The angular momentum operators are therefore 3X3 matrices.
For example lets calculate the basic commutator.

Ppt 16 Angular Momentum Powerpoint Presentation Free Download Id
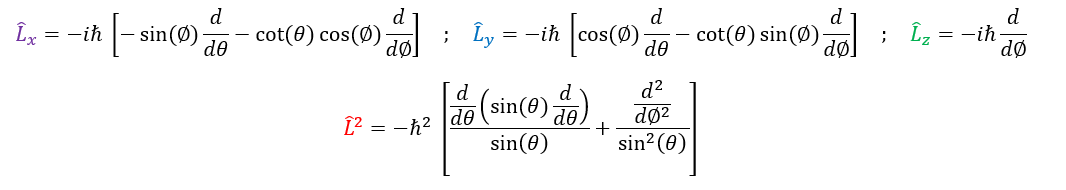
Angular Momentum Operators
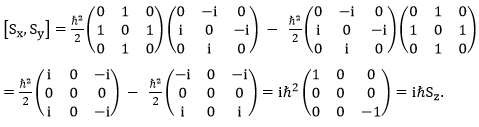
Properties
Spin Angular Momentum Operator のギャラリー
Quantum Diaries

Angular Momentum Operator Introduction To Quantum Mechanics Exam Docsity
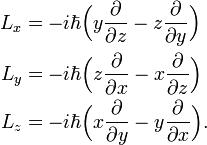
Angular Momentum Quantum Knowino

Rank 2 Spin Tensors
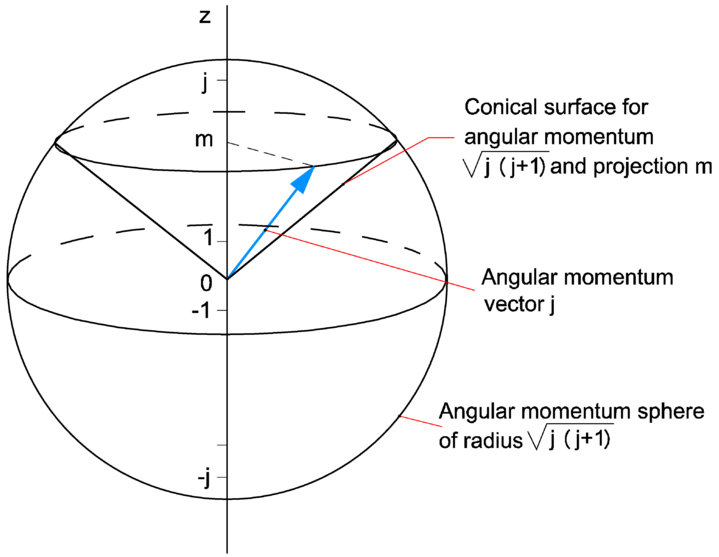
Quantum Diaries

Angular Momentum Operator Wikipedia

Adding Angular Momenta

Pdf On Angular Momentum Operator In Quantum Field Theory

Angular Momentum

Angular Momentum Book Chapter Iopscience
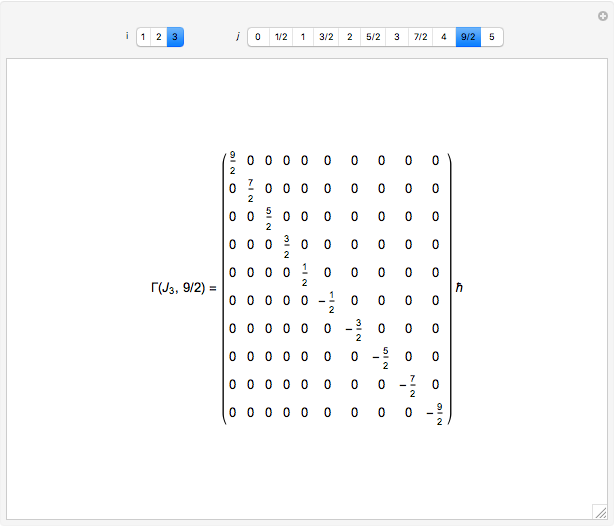
Quantum Angular Momentum Matrices Wolfram Demonstrations Project

Angular Momentum Notes

Angular Momentum Hydrogen Atom And Helium Atom Spin Physics Boson

Solved The Spin Angular Momentum Operators For A S 1 2 Chegg Com
2
2
2

Angular Momentum Book Chapter Iopscience

Ppt Spin And Addition Of Angular Momentum Powerpoint Presentation Free Download Id

Why Do We Relate Spin With Angular Momentum Operator In Quantum Me
2

Total Angular Momentum An Overview Sciencedirect Topics
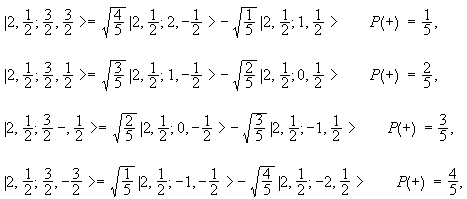
Addition
Tbp Berkeley Edu Exams 4434 Download

Atomic Physics Part Phys261

Electron Spin Electron Spin Hypothesis Ppt Video Online Download

Angular Momentum Operator Algebra Youtube

Angular Momentum

Angular Momentum Ladder Operators

Spin Angular Momentum Of Light Wikiwand
Q Tbn 3aand9gcqx Gjvxrrqdiu49v40wbszetypi14zlrt9lx2qn1h Kiqxbm Usqp Cau
Angular Momentum Operator Quantum Mechanics Spin Png 1280x948px Angular Momentum Operator Angular Momentum Area Art Bohr
Www3 Nd Edu Johnson Class01f Chap1a Pdf

Angular Momentum Book Chapter Iopscience
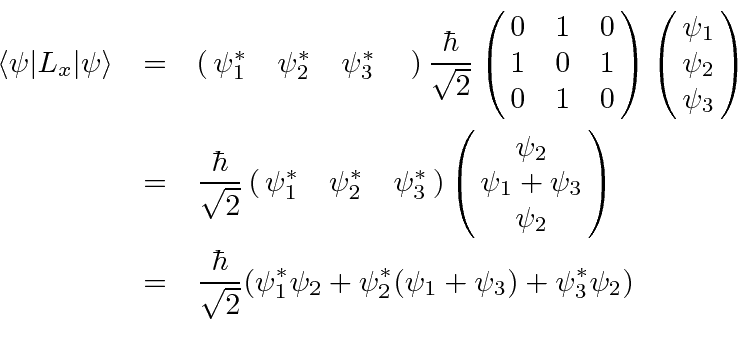
The Angular Momentum Matrices

Slideshow And Powerpoint Viewer The Periodic Table See Shankar Pp 369 371 Griffiths Sect 5 2 2 Understanding The Periodic Table Is One Fo The Triumphs Of Qm Recall That For Hydrogen The Ele
Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 5 4484 Rep Rep1 Type Pdf

Angular Momentum Notes
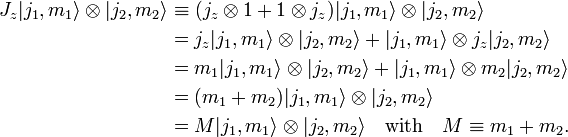
Angular Momentum Coupling Knowino

Quantum Mechanics 4 Angular Momentum And Spin Lecture Notes And Qs Studocu

Pdf Spin And Angular Momentum Operators And Their Conservation
Http Www Hep Lu Se Staff C Jarlskog Chapter4 Pdf

Solved For Two Electrons The Z Component Of The Total Orb Chegg Com

Chapter 9 Spin Total Angular Momentum Let Us Recall Key Results For The Total Angular Momentum 6 B 2 6 C Ppt Download

Answered A Particle Of Spin Is Described By A Bartleby

Quantum Theory Of Angular Momentum Angular Momentum Operators Pdf Document

Why Must Angular Momentum Operator Annihilate The Vacuum Physics Stack Exchange

Orbital Angular Momentum Advanced Quantum Chemistry And Spectroscopy Lecture Slides Docsity

Quantum Angular Momentum
Http Joelcorbo Com Docs Notes Spin Pdf

Orbital Angular Momentum Ppt Download

Angular Momentum And Spin Spin Physics Eigenvalues And Eigenvectors

Spin Orbit Coupling

The Total Z Component Of The Spin Angular Momentum Chegg Com

Solved 2 Spin Angular Momentum Operators For 2 And Three Chegg Com
Arxiv Org Pdf 1410 0468
Vector Model Of Angular Momentum
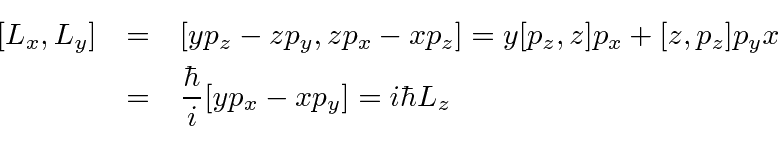
The Commutators Of The Angular Momentum Operators
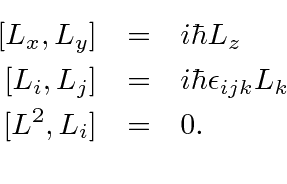
Angular Momentum Algebra Raising And Lowering Operators

Table 1 From A Complete Product Operator Theory For Is I 1 S 1 Spin System And Application To 3d Hmqc Cosy Nmr Experiment Semantic Scholar

Note 5 Spin Angular Momentum

Ppt Angular Momentum In Quantum Mechanics Powerpoint Presentation Free Download Id

Spin 1 2 Youtube

Solved 5 Consider An Angular Momentum Operator ſ Such A Chegg Com

Lecture 5 Orbital Angular Momentum Spin And Rotation 1

The Total Z Component Of The Spin Angular Momentum Chegg Com
2
Http Www Physik Fu Berlin De En Einrichtungen Ag Ag Eisert Teaching Qmchapter7 Pdf

Pdf Angular Momentum And Spin Dr J M Ashfaque Amima Minstp Academia Edu
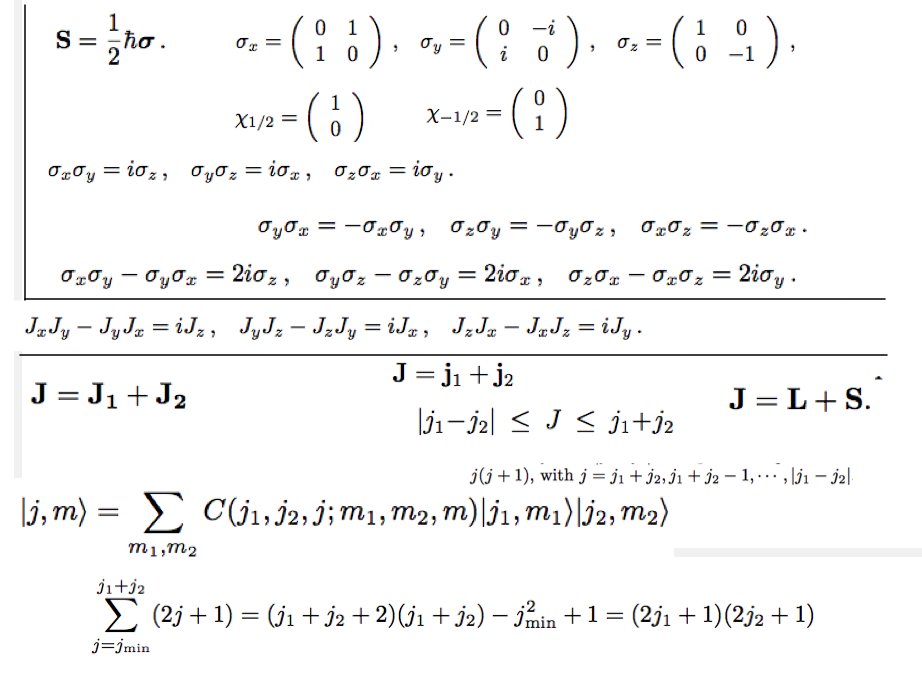
Atomic Physics Part Phys261

Pdf Spin And Orbital Angular Momentum Of Photons

Lecture 14 Generalised Angular Momentum And Electron Spin
Onlinelibrary Wiley Com Doi Pdf 10 1002 App2
Q Tbn 3aand9gcqgh0qcg0c1yrkrdfsovceqecn3gpvhhhdnaiubf 9zoeljrgou Usqp Cau
Arxiv Org Pdf 03
What Is The Formula For Spin Angular Momentum Quora
Q Tbn 3aand9gct4n Qjkwskav71p1et8ac0ufbcihtzfuecsvg1 Ggdfzsauuim Usqp Cau

Total Angular Momentum Quantum Number Azimuthal Quantum Number Angular Momentum Operator Angular Purple Angle Leaf Png Pngwing
2

Angularmomentum
Www Studocu Com En Gb Document University Of Hertfordshire Physics Lecture Notes Quantum Mechanics 4 Angular Momentum And Spin Lecture Notes And Qs View
Q Tbn 3aand9gcrkwfbautxvico7f1wrt7 Os3gke9da5vqa3mjr1geh4irxqx Usqp Cau

Talk Angular Momentum Operator Wikipedia

Find The Eigenvalue Of The Total Spin Angular Momentum Operator S 2 2 Find The Eigenvalue Of Homeworklib

Pdf Angular Momentum In Quantum Mechanics Omer Gassim Academia Edu

Angular Momentum Eigenfunctions Youtube
Tbp Berkeley Edu Exams 4434 Download
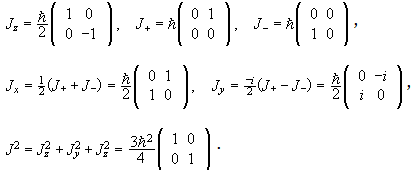
Properties

Quantum Angular Momentum
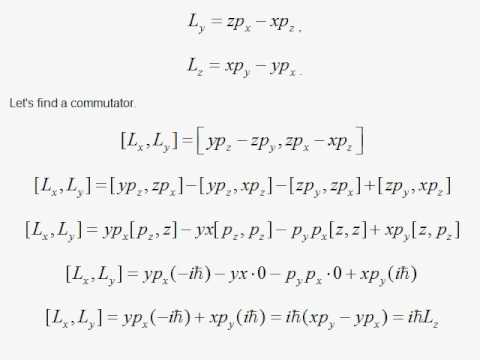
K3 Angular Momentum Youtube

Pdf Angular Momentum And Spin In Quantum Mechanics A Review Dr J M Ashfaque Amima Minstp Academia Edu
Www Chem Tamu Edu Rgroup Hughbanks Courses 634 Handouts Angular Momentum
Http Physik Kfunigraz Ac At Uxh Teaching Questionnaire Aqm1 Pdf

Chapter 11 Angular Momentum General Theory
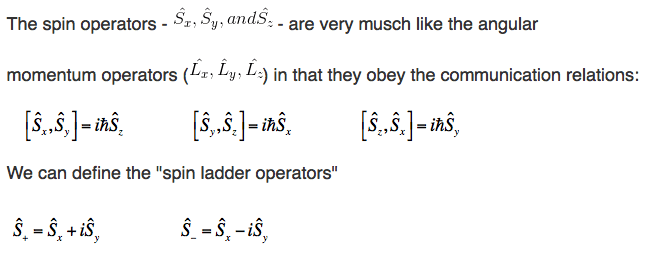
Oneclass Questions The Spin Operators Sr Su Ands Are Very Musch Like The Angular Momentum Operato
2
Http Www Indiana Edu Ssiweb C561 Pdffiles Ang Mom Pdf

Angular Momentum Operator Wikipedia

Symmetric Angular Momentum Coupling The Quantum Volume Operator And The 7 Spin Network A Computational Perspective

Quantum Mathematics 34 4 Operators For Spin Angular Momentum Youtube

Solved 2 30 The Total Z Components Of The Orbital And Chegg Com



